中心角の求め方が即わかる&合わせて知りたい知識とは? 数学における 中心角の求め方について、早稲田大学に通う筆者が丁寧に解説 します。 数学が苦手な人でも中心角の求め方が理解できるように、スマホでも見やすいイラストでわかりやすく解説し動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ 練習問題 各単元の要点 pcスマホ問題 数学の例題 中1 計算問題アプリ 正負の数 中1数学の正負の数の計算問題 加法減法乗法除法累乗四則計算 中2数学

中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット
中2 数学 角度の求め方 応用
中2 数学 角度の求め方 応用- 芸術的な難問 良問数学 中2数学 複雑な多角形 角の和応用問題 今回は複雑な多角形の角の和の問題とその考え方です 星型など複雑な図形の角の和を求めるとき三角形の外角の定理やブーメラン型四角形の角リボン型ちょうちょ型の三角形の角の考え方が役立ちます 中2数学「多角形の角」の問題 どこよりも簡単な解き方・求め方 今回は「多角形の角」を学習します 基本的なところは算数で学習しましたね 「三角形の角の性質」「多角形の内角(外角)の和」「へこみのある図形の角度」について一緒に見ていきましょう




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
単元 立体の体積と表面積, 「立体の角度・面積・体積の求め方を自分なりにノートにまとめてみました! 見にくかったり、イマイチ分からないという方はゴメンなさい‥‥!ω・`)」, キーワード 中1,数学,円錐の角度・面積の求め方,円柱の面積・体積の求め方,角錐の面積・体積の求め方, 中2*数学 角の大きさの求め方 >>応用問題あり 中2の証明です、学校からの課題なんですが、全く分からないのでどなたか教えてくれませんか😭 中2数学「いろいろな連立方程式の計算」の問題 どこよりも簡単な解き方・求め方 21年8月12日 kazunokazu かずのかずブログ
名文模写って文章上達に効果あるの おすすめの書き写し法 手本5種 文章力読解力を破壊しないために最初に避けるべきポイントを紹介してみます 新聞コラムの書き写しの持つ危険性 1文章には様々なパターンがあり漫然と書くと混乱する 文章には論理的な文章と文学的な文章があり 中3数学 中学数学円錐の高さの求め方がわかる3ステップ 中2数学 中2数学サイコロの目の確率を3秒で計算できる公式 中2数学 文字式の利用連続する3つの整数の和が3の倍数になる証明 中3数学 165中3数学平方根を含む乗法(掛け算)のやり方を解説します! 中学生の勉強方法 190 中1数学比例のグラフの書き方とそのグラフの特徴について知ろう!(その2) 中学生の勉強方法 2176 中2数学樹形図を使って簡単に確率を解く方法を解説!
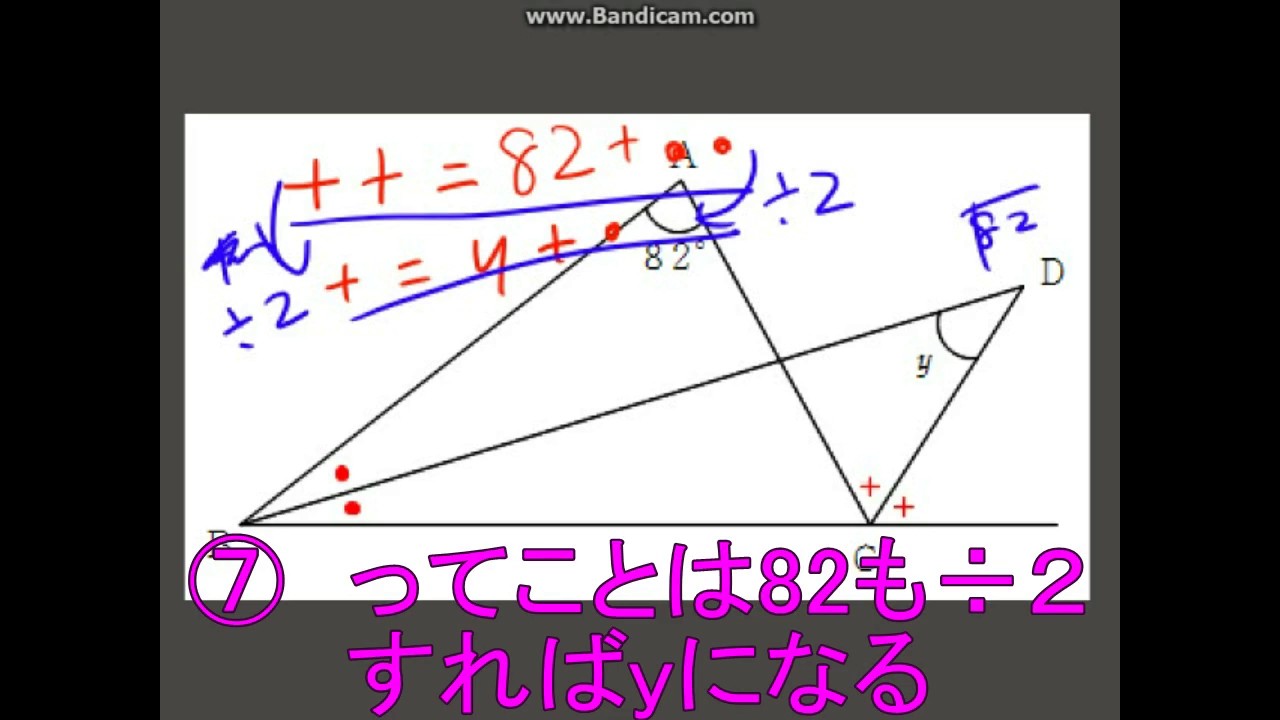
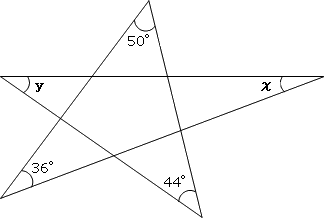
すると、図の角度が分かるね。 ここから、三角形の 外角の定理 を使うと、 ∠x+50°=100° となるよ。 ちなみに、この三角形の 2辺は円の半径 でできている、つまり 二等辺三角形 になっていることから、答えを求めることもできるよ。 (1)の答え中2数学 ブーメラン型角度の求め方を解説 数スタ 中学数学 求角と方程式 中学数学の無料オンライン学習サイトchu Su ラングレーの問題 整角四角形 星形の角度の求め方がわかる3つのステップ Qikeru 学 中2です!xの角度の求め方を教えてください! まず(3)から ABDは二等辺三角形より角BAD=角ABD=xそうすると角BDCは ABDの外角だから角BAD角ABD=角BDCなのでxx=2x BDCも二等辺三角形なので角BCDも2xまた ABCも二等辺三角形なので角BCD=角ABC=2xよって三角形の内角の和が5x=180になりx=36(4)は角ACB=70°で BACは二
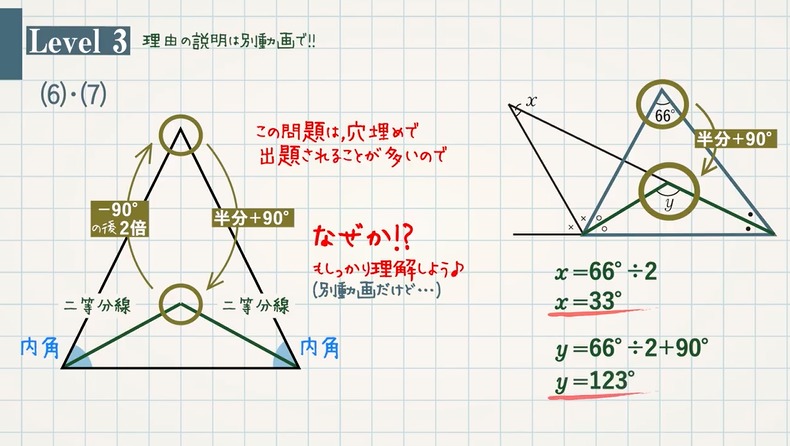



角度の計算 裏技まとめ 教遊者
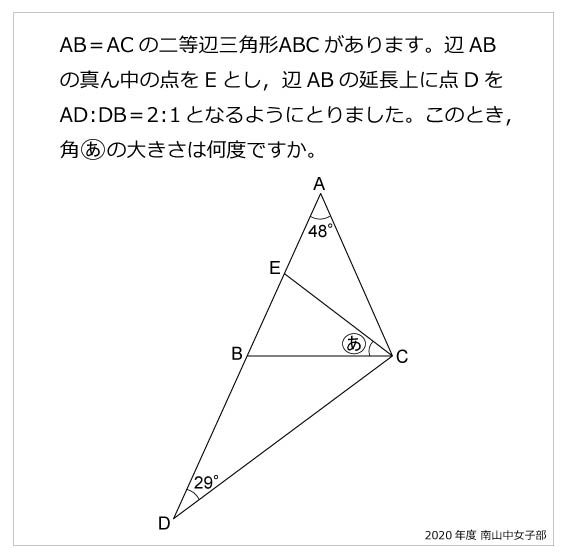



角度 算数星人のweb問題集 中学受験算数の問題に挑戦
問題3 下の図の角xの角度を求めなさい。 → 解答 問題4 下の図の角xの大きさを求めなさい。ただし、同じ印の付いた角の大きさは等しいものとします。解答課題学習の指導(数学) 1. 教材 「星形多角形の内角の和を追究しよう」(2年) 2. 教材観 三角形や多角形の内角の和を学習した後で,発展問題としてよく扱われる教材である。 星形五角形だけとっても,その形のきれいさで生徒の興味・関心を 中3数学因数分解の利用ででてくる2つの問題 中3数学 二次方程式の利用面積の文章問題の解き方がわかる4ステップ 中2数学 152 一次関数直線の式がわかる4つの求め方 中1数学
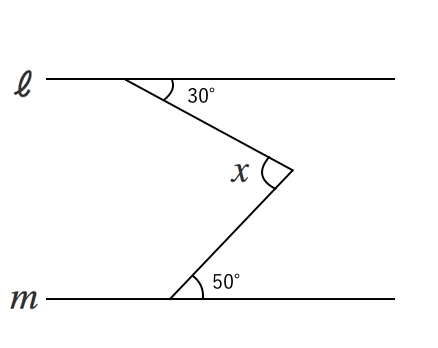



図形の調べ方 角度を求める問題 苦手な数学を簡単に
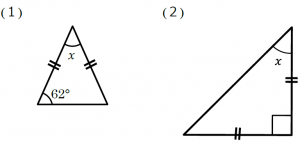



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン
中2数学"合同"ってなに?数式で合同を表すにはどうしたらいい? 中学生の勉強方法 131 中3数学解の公式とその導き方を知って、2次方程式をマスターしよう! 中学生の勉強方法 115 中2数学文字を含んだ図形の体積の求め方とは? 平行四辺形の性質 長さ 角度の問題 無料で使える中学学習プリント 難問に挑戦しよう Geogebra 平行四辺形の書き方 コンパスを使って作図する方法は 数スタ 角度 図形問題 正三角形を作る 数学難問 平行四辺形 Youtube 超難問 図の角度 の大きさを求めよ 平面 図形 角度の求め方 中2 34 画像の図形の内角の和は900度なのですが 求め方が分かりません。 答えの式には180(72)=900 となるのですが、なぜ七角形になるのでしょうか? 分かる方ご回答お願いします。 数学・算数



1



角度問題の教え方1 中2知識の問題の基本方針 塾講師 数学マンは踊る
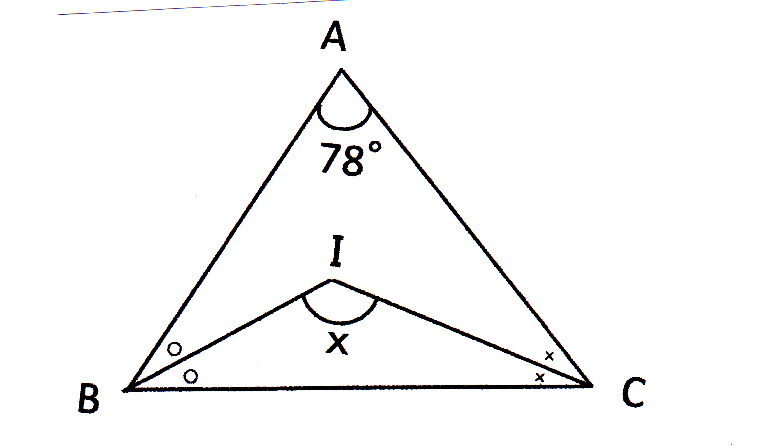
中2数学ブーメラン型角度の求め方を解説! ツイート シェア はてブ LINE Pocket この形の図形っって 角度を求める問題でよく出てくるよね。 ブーメランの形に似ているから 『ブーメラン型の図形』 って呼ばれたりしています。他に 中2数学です。角Xの大きさの求め方を教えてください。同じ印のついてる角の大きさは等しいです(1)赤い三角形について、右側の底角の大きさは、 青い三角形について、x=180 ( )=54 また、赤い三角形について、2 =5 中 2 数学 角度 の 求め 方 中 2 数学 角度 の 求め 方・・・(答え) ほら同じになるでしょ?! だから 三角形の1つの外角は、その隣にない2つの内角の和と等しい 外角は対頂角になっている中2数学の質問です。 下の図の問題は3つとも、 ∠bacの角度は∠bdc
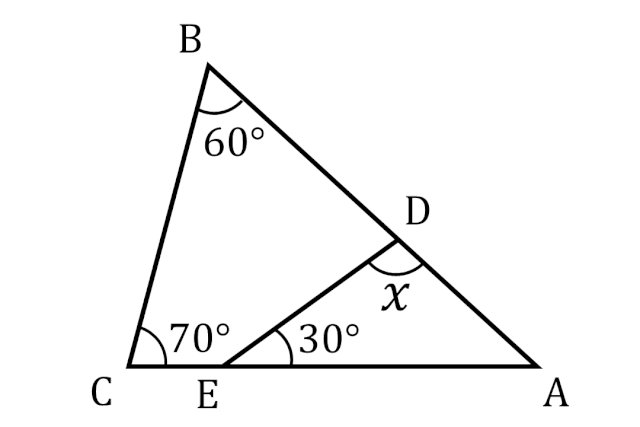



毎日脳トレ 中2レベルだけど簡単 図のxの角度は Dアプリ レビュー




図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に
計算問題も徹底解説 21年1月日 この記事では、三角関数について、角度の求め方や変換公式(\(90^\circ − \theta\) など)について解説していきます。 この \(2\) つを押さえておけば、単位円の中に直角三角形を 図形 角度の求め方 中2 Okwave 中 2 数学 角度 の答え 二等辺三角形が2つくっついている問題ですね。 この場合、それぞれの二等辺三角形に注目して角度を1つずつ求めていきます。 赤い二等辺三角形は、頂角が36°なので 底角1つ分の角は となります。 そこから、次は青い二等辺三角形に注目して を 中2数学の角度の求め方について質問です 25°以外全く角度がわかりませんどう求めればいいのでしょうか・・・ 外角とその内角以外の2角の合計が等しくなる定理を使います。もし分かりにくかったら ABCにおいて∠A∠ABC=∠ACE①になるという関係です。同じく∠D∠DBC=∠DCE②に
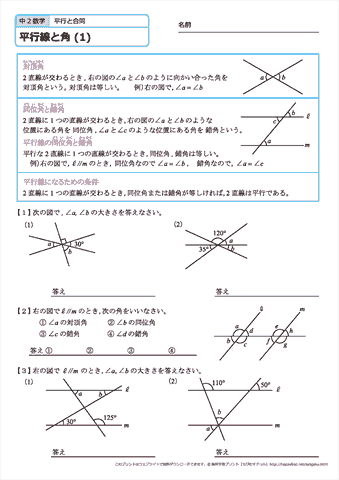



中学2年生 数学 平行線と角 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット
図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に 角度の難問 中学生版 中2数学 対頂角 同位角 錯角と平行線の関係 中2数学 ブーメラン型角度の求め方を解説 数スタ 外角の和=360° (多角形の外角の和は、辺の数にかかわらず360°)です。 1つの内角1つの外角=180° (となりあう外角と内角は180°)です。 1つの外角=360÷n 1つの内角=180°1つの外角=180°(360/n) 二等辺三角形の角度の問題では 底角が等しいこと 三角形の外角の性質 この2点を覚えておけば応用問題でも解くことができます。 ただし、発想が難しい問題もあるので、いろんな問題集を使って知識を深めておきましょう。 スポンサーリンク




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ



中2数学の角度の求め方について質問です 25 以外全く角度がわかりませんど Yahoo 知恵袋
角度問題の教え方1 中2知識の問題の基本方針 中学数学 どの試験でも角度を求める問題(以下角度問題)は頻出です。 角度の問題は入試では円周角と絡めて出題されることが多いです。 その円周角を習うのは中3の後半です。 夏季に角度問題を対策する 角度の求め方 算数の教え上手 学びの場 Com 中学二年 数学図形の問題です Xの角度の大きさが50 になる理由を 円の中の角度02 数学教材 Studydoctor二等分線の角度の問題 中2数学物理公式集 中・高生の孫はこの計算式を教える前に26度と回答していました Googleマップで自宅・国立競技場間の距離を測って、このサイトで角度を求めました。度ぐらいとわかりました。




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
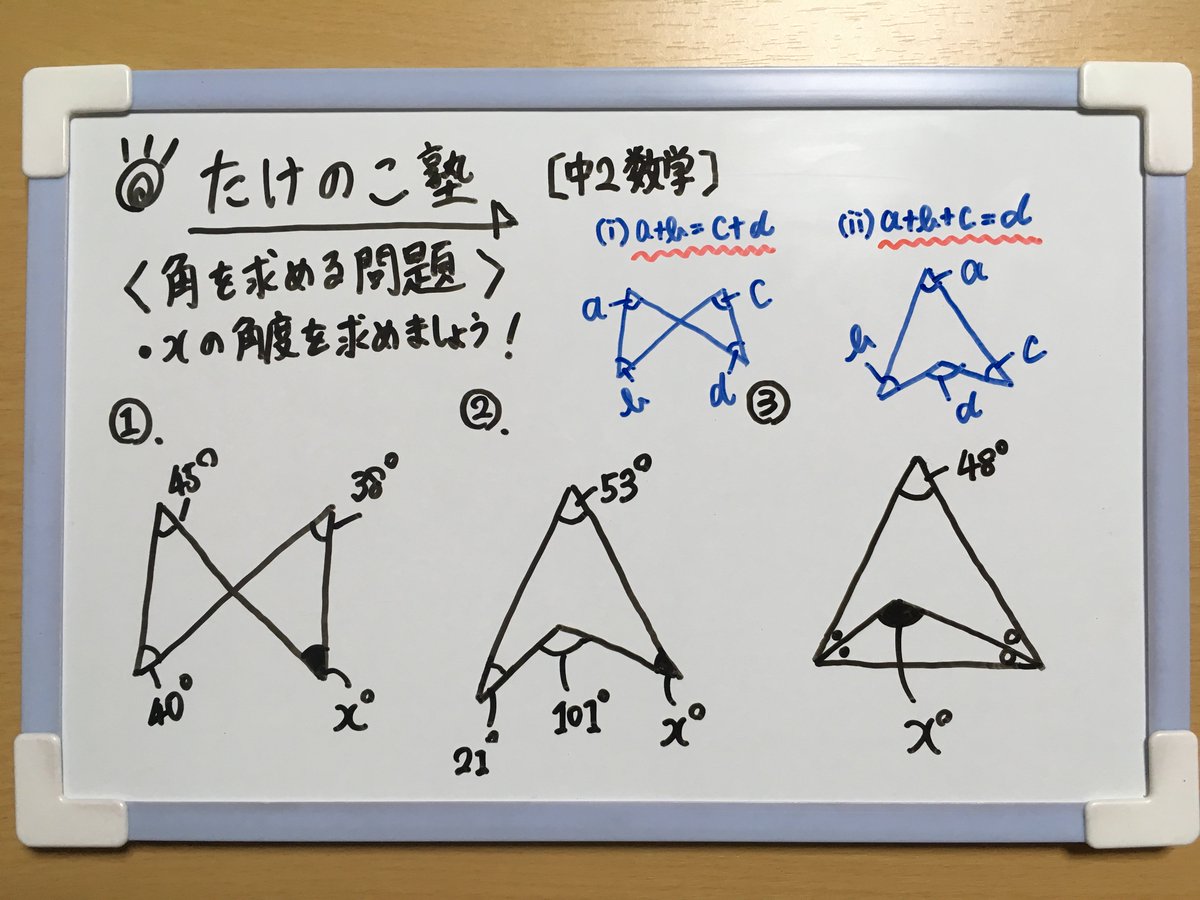



たけのこ塾 En Twitter 中2数学 今回は 角度を求める問題 を作成しました 定期テストなどでよく出題される問題を取り上げてみましたので ぜひチャレンジして下さいね 詳しくは画像の解説をご覧下さい 勉強垢 中2 数学 図形の調べ方 Youtube
中2 数学 角度 問題 2349中2 数学 三角形 角度 問題 式 計算問題アプリ 連立の計算問題 基礎から標準問題までの練習問題と、例題による解き方の説明中3 数学の因数分解についてです。 (例)18ⅹ²-12xy=6x(3x-2y) この問題の途中式で、18は2×9, 12は2×6で共通次の図で印をつけた角度の合計は何度になるか求めよ。 練習問題 各単元の要点 pcスマホ問題 数学の例題 学習アプリ 中2 連立方程式 計算問題アプリ 連立の計算問題 基礎から標準問題までの練習問題と、例題による解き方の説明 解説 まず、二等辺三角形がたくさん見つかることがわかるよね! だから、二等辺三角形の特徴である " 2 2 角が等しい" を利用してみるよ。 すると、こんな風に文字を置けるね! はい、カラフルになりました。 ここからどうすればいいかわかるかな



1



円と三角形 角度 中学から数学だいすき



Math 平行と合同 角の二等分線と角度 働きアリ




の角度を求める問題です 教えて下さい Clear




簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
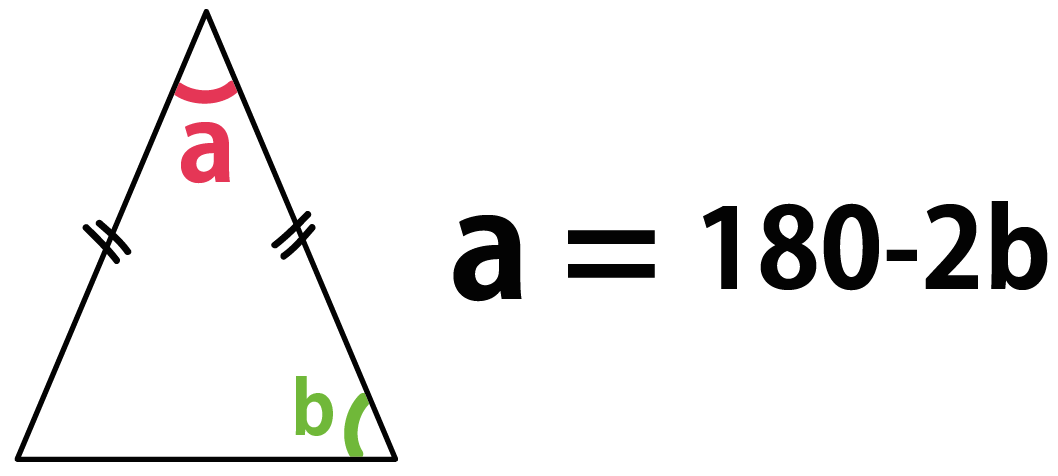



簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく




中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



三角形内の角度を求める問題 現役塾講師のわかりやすい中学数学の解き方



Math 角度の難問 中学2年生 働きアリ




角度の求め方 算数の教え上手 学びの場 Com



1




三角形の角度を求める問題 小学生 中学生の勉強
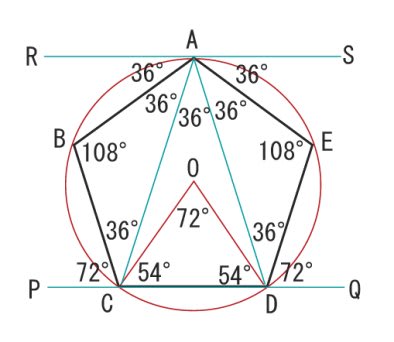



正五角形というだけで 分かる角度は 名寄 算数数学教室より




多角形の内角の和 外角の和の公式 数学fun
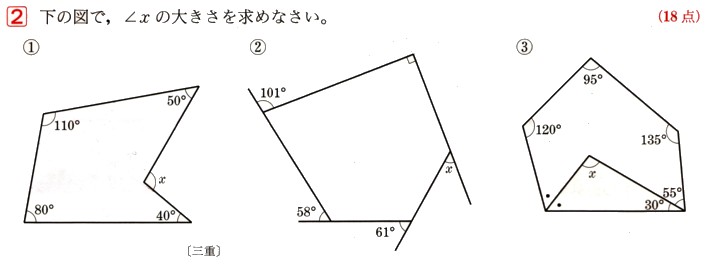



中学2年数学 図形の調べ方 三角形 多角形と角 確認問題2 解答 あんのん塾




中学数学の図形の角度を求める問題です 次の問題が分かりませんでした 数学 教えて Goo
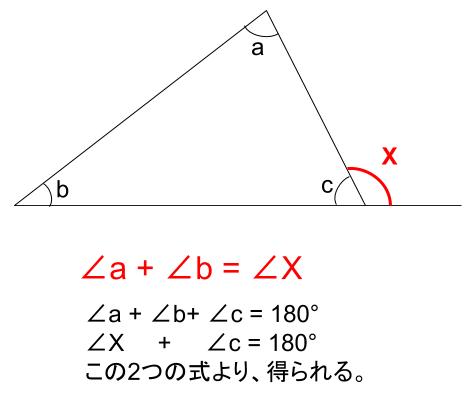



中学数学 三角形の内角 外角 中学数学の無料オンライン学習サイトchu Su




中2 角度の求め方 勉強 Youtube スタディチューブ




中学校2年生数学 いろいろな角度の求め方
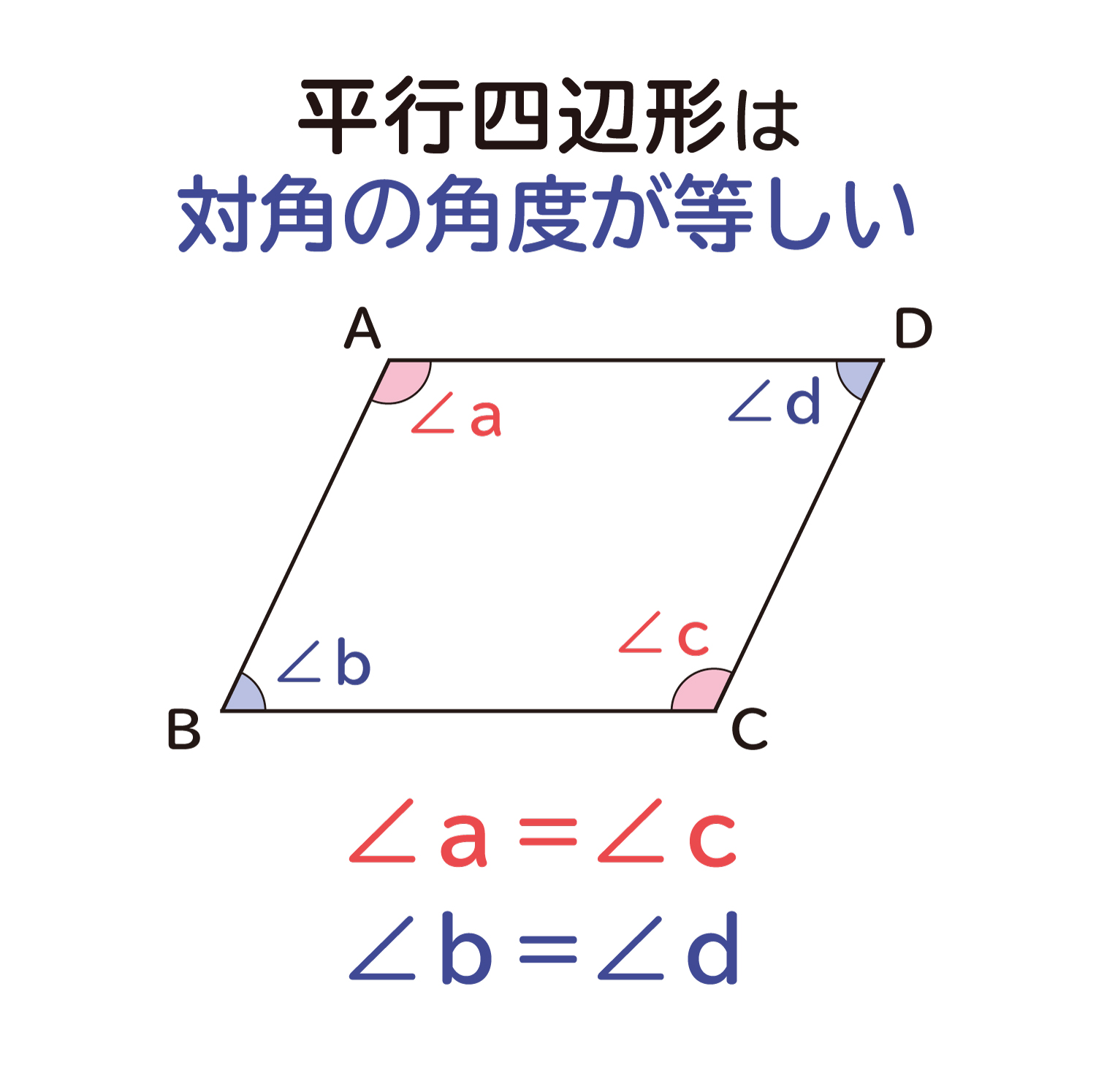



平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル




ちょうちょ型図形の角度は 求め方を徹底解説 数スタ



中2の数学の問題です Xの角度の求め方がわかりませんどなたか教えてください Yahoo 知恵袋




角度の計算 裏技まとめ 教遊者




中学2年生 数学 星形の図形の角度の求め方 我流舎ウェブかわら版 川西市山下 個別指導塾 我流舎のブログ




中2 数学 4 2 三角形の角度の利用 Youtube



三角形の角度を求める 思考力を鍛える数学
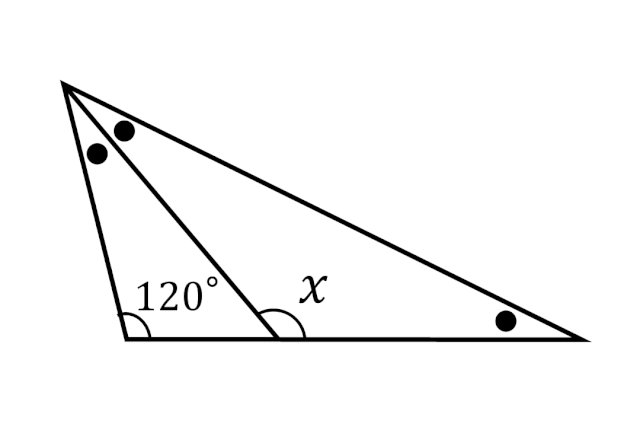



今週の人気脳トレbest 5 中2の数学に挑戦 Xは何度 Nttドコモ Dアプリ レビュー




多角形の内角の和の公式と外角の和を利用した角度の求め方
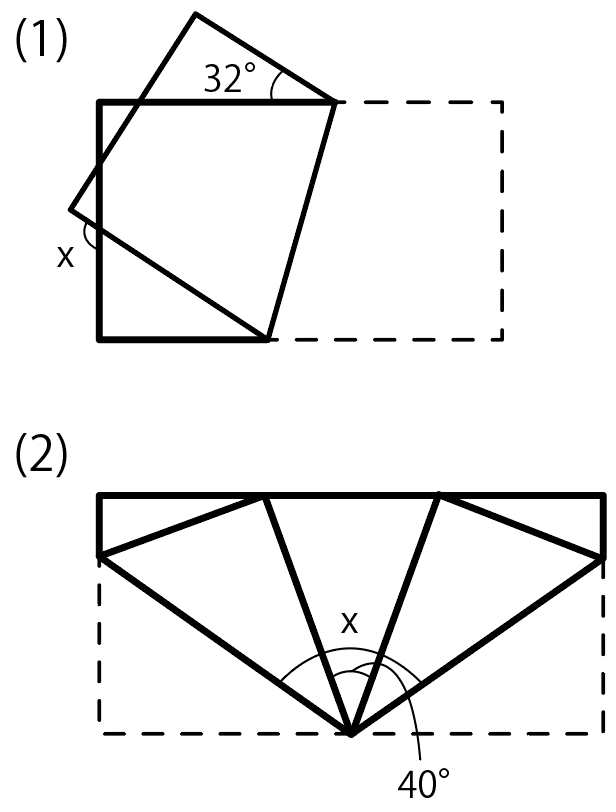



折り返した図形の角度を求める2つのコツ Qikeru 学びを楽しくわかりやすく
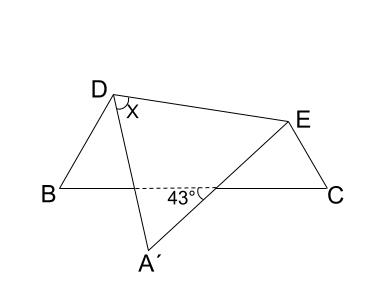



中学数学 求角 折り返し 中学数学の無料オンライン学習サイトchu Su



超絶難問 ラングレーの問題 時習館 ゼミナール 高等部




角度の問題まとめ 無料で使える中学学習プリント
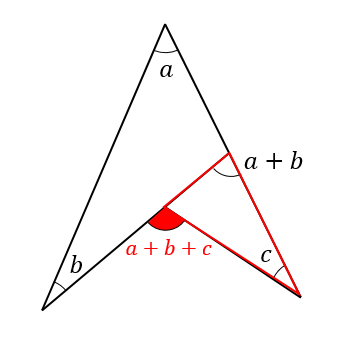



中2数学 ブーメラン型角度の求め方を解説 数スタ



Studydoctor二等分線の角度の問題 中2数学 Studydoctor



中学生の数学 角度の問題




三角形の角度を求める問題 小学生 中学生の勉強



Studydoctor多角形の角度の問題 中2数学 Studydoctor




中2数学 複雑な多角形 角の和 応用問題



千葉県松戸市の個別指導塾 ナビ個別指導学院馬橋校ホームページ 中学2年生数学 角度の求め方
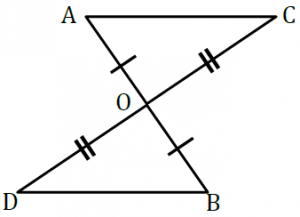



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン
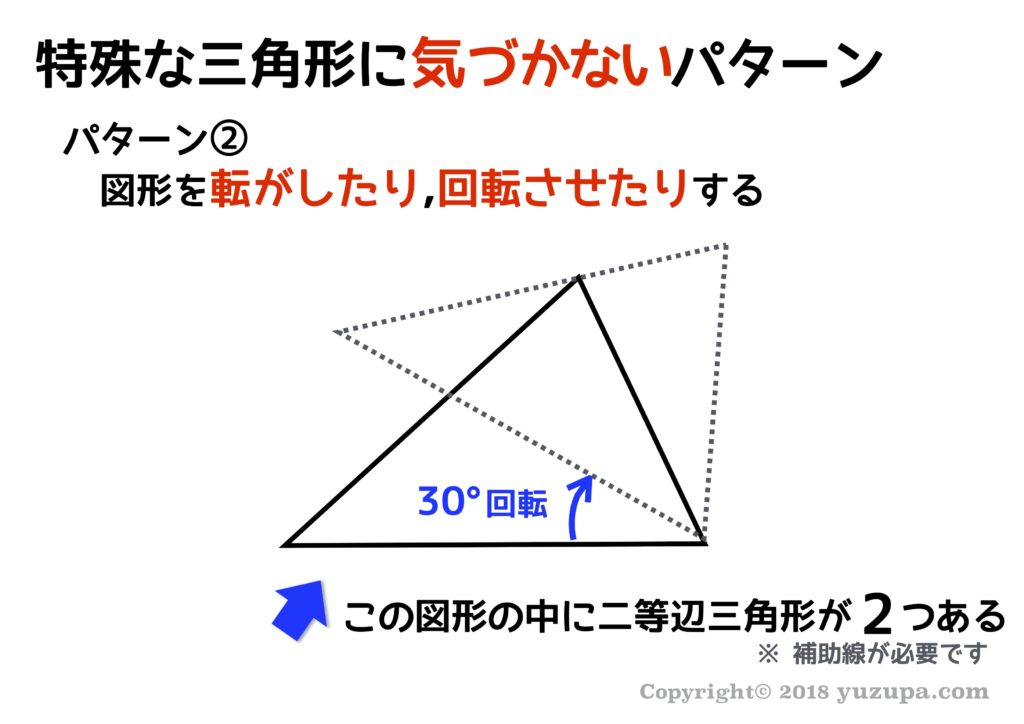



中学受験 図形の角度問題は 7つ道具 で攻略 かるび勉強部屋




角度を求める問題 スリッパを探そう 苦手な数学を簡単に
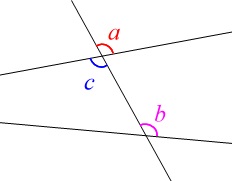



平行線の同位角と錯角を利用して角度を求める問題の解き方




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学




数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中学校2年生数学 いろいろな角度の求め方



Math 平行と合同 角の二等分線と角度 働きアリ



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典
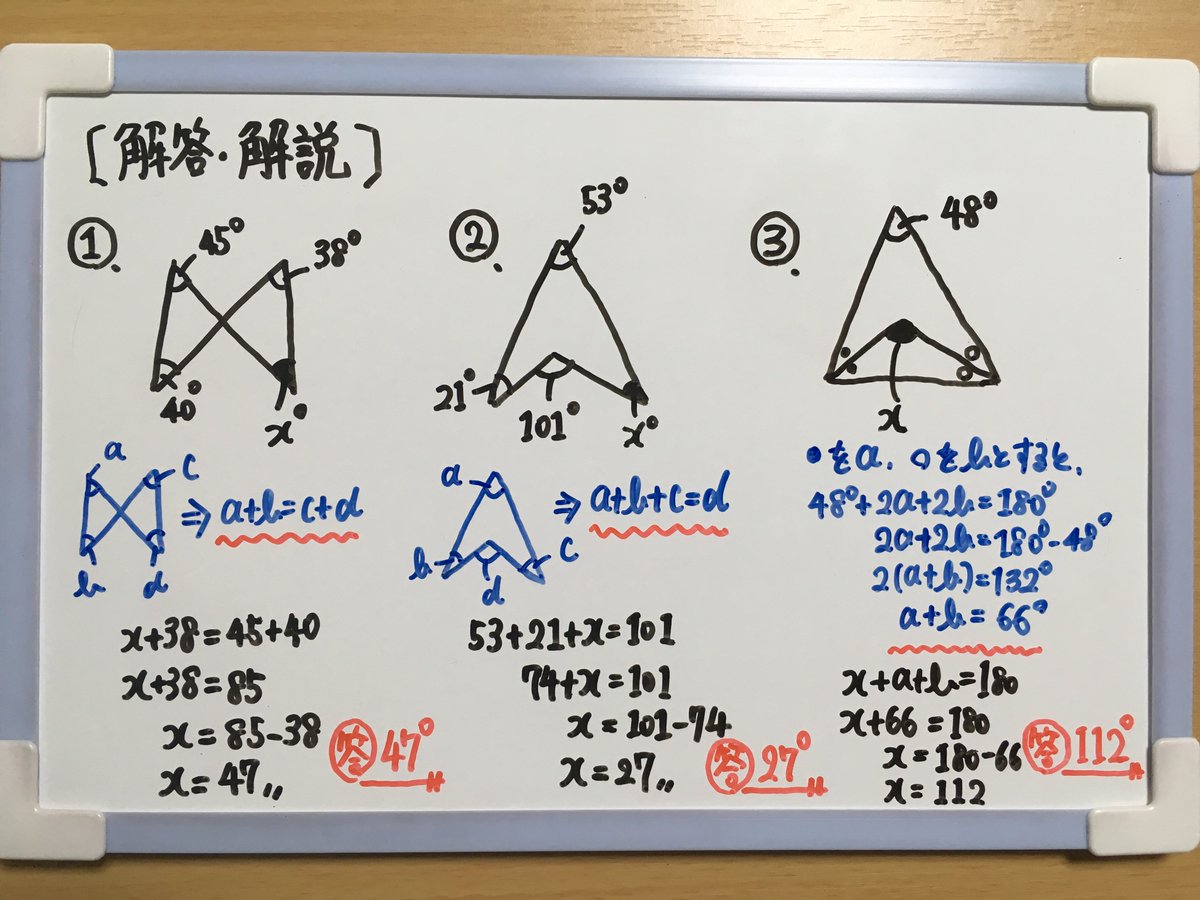



たけのこ塾 中2数学 今回は 角度を求める問題 を作成しました 定期テストなどでよく出題される問題を取り上げてみましたので ぜひチャレンジして下さいね 詳しくは画像の解説をご覧下さい 勉強垢 中2 数学 図形の調べ方 Youtube



Studydoctorブーメラン図形の角度 中2数学 Studydoctor




錯角 同位角 対頂角の意味とは 平行線と角の性質をわかりやすく証明 応用問題アリ 中2数学 遊ぶ数学
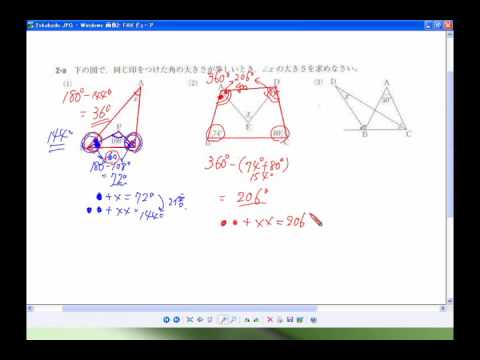



中2数学 角度応用 1 Youtube



Studydoctor星形図形の角度 中2数学 Studydoctor
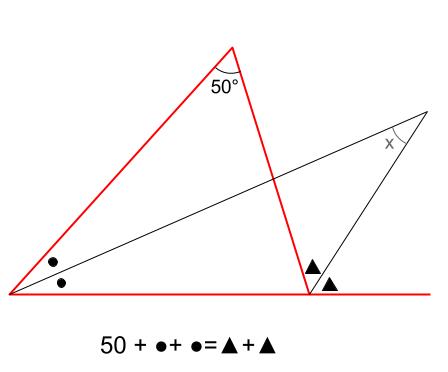



中学数学 求角と方程式 中学数学の無料オンライン学習サイトchu Su




数学 中2 53 角度チャレンジ Lv 1 Youtube




星形の角度 内角の和の求め方を問題解説 数スタ
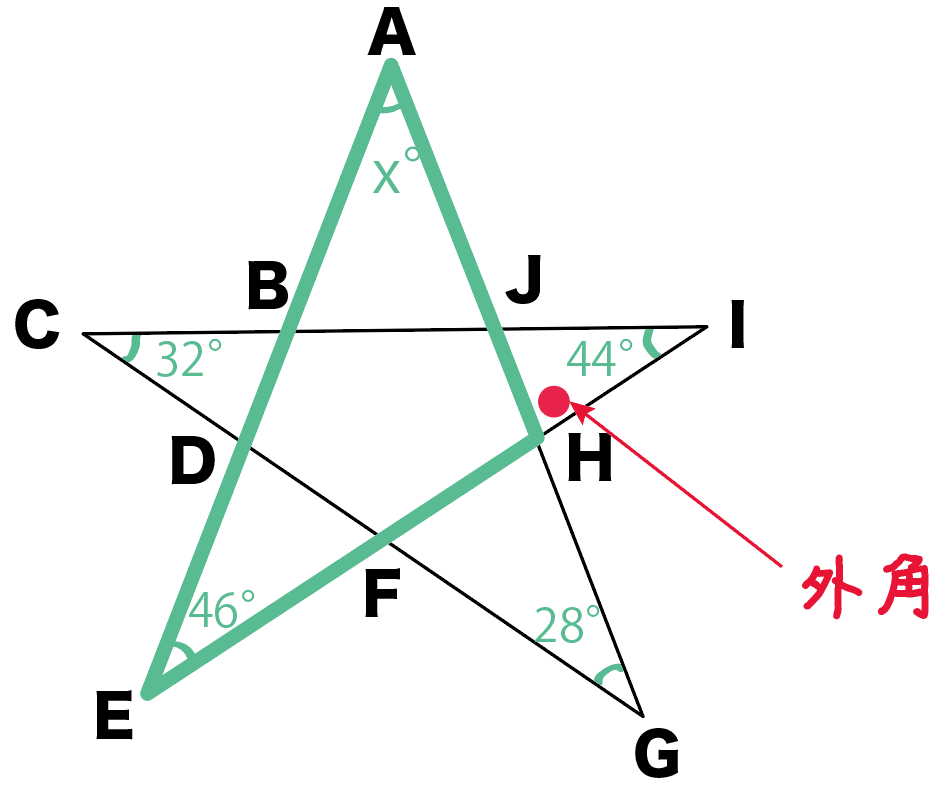



星形の角度の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット




中2数学 これらの角度の求め方 答えを教えてください Clear




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット
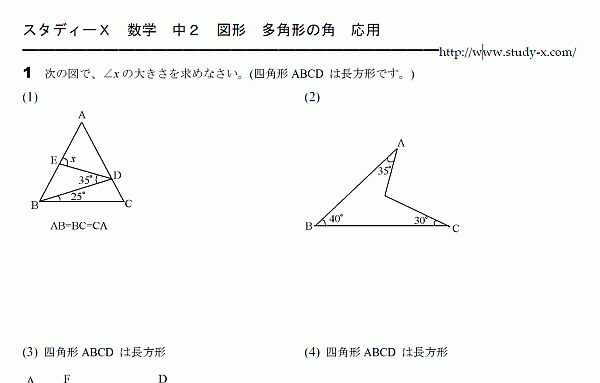



中2 数学 無料学習プリント教材
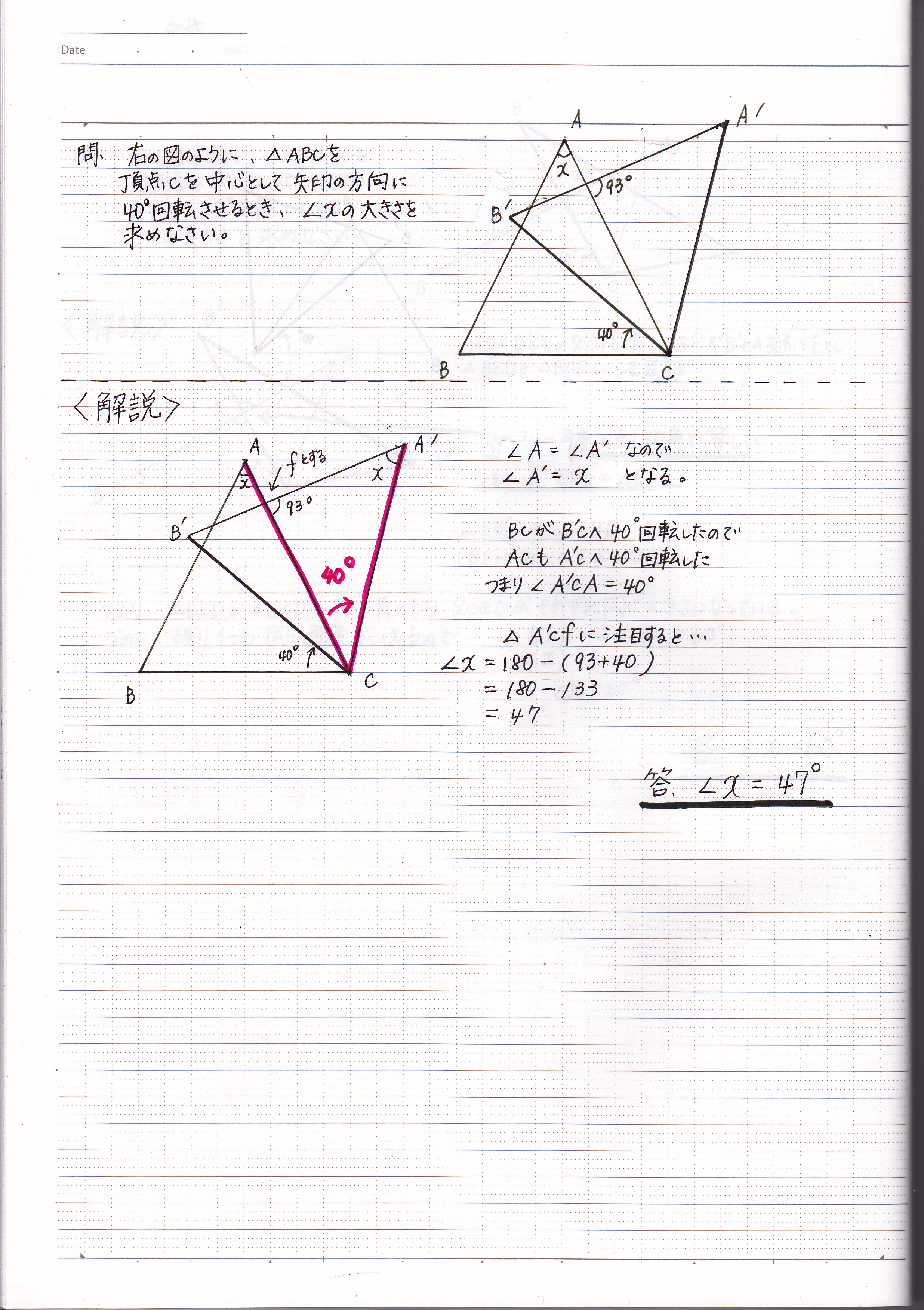



回転する図形の角度の求め方 現役塾講師のわかりやすい中学数学の解き方



中2の数学の多角形の問題で この図形のyの角度の求め方を教えてください Yahoo 知恵袋



紙ヒコーキ型図形の角度を求める 平行線と角 勉強ナビゲーター




余弦定理で角度を求める方法 数学の星



中学二年 数学 三角形の角度の求め方 中の上編 Youtube




外角の求め方 外角の和を使って多角形の角度を求める問題 中学や高校の数学の計算問題
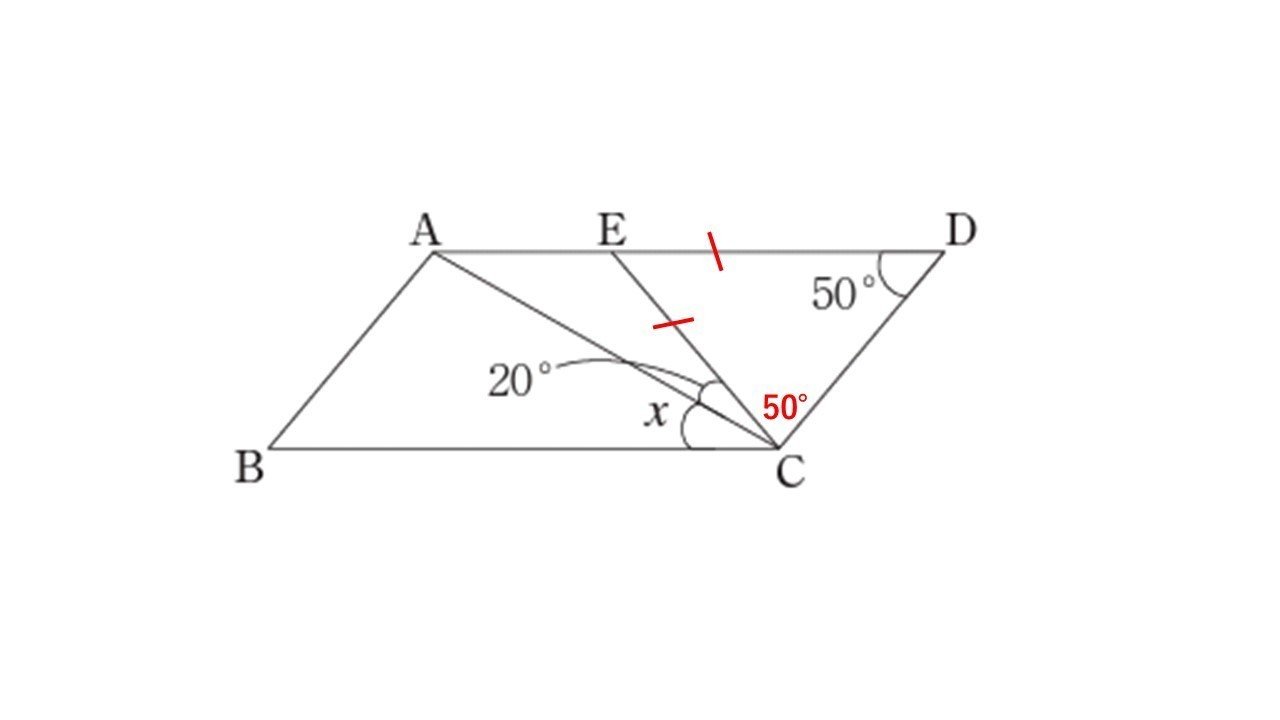



中学数学の平面図形の角度を求める問題を通して学び直しする論理 数学の基礎 タロウ岩井の数学と英語 Note




中2数学 複雑な多角形 角の和 応用問題
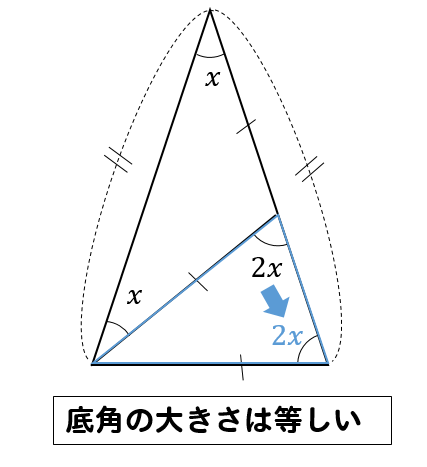



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ




中学数学 平面図形と角度 の二等分線の裏技教えます 前半 中2数学 Youtube



角度の難問 中学生版



Q Tbn And9gct2skgsrke4pile7gcesp I7jw94vcxtdg9ansg6w8efqa Y Rv Usqp Cau
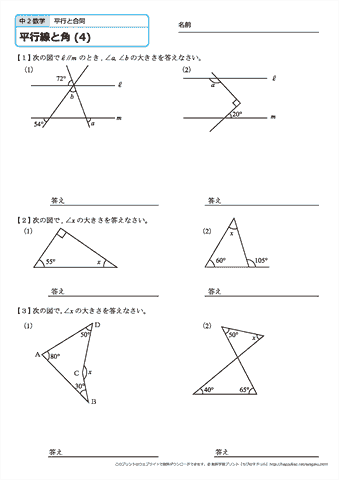



中学2年生 数学 平行線と角 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



角度の求め方 算数の教え上手 学びの場 Com
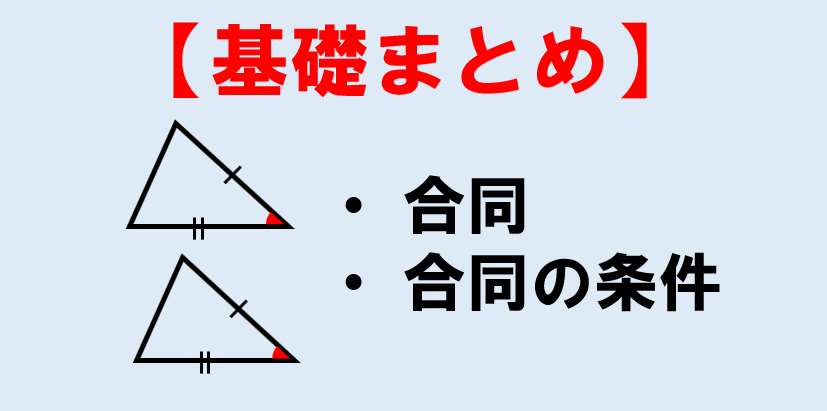



中2数学 合同 三角形の合同条件まとめ 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト



正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典




角度の問題まとめ 無料で使える中学学習プリント




中学2年の数学 動画 角度チャレンジ Lv 1の問題 19ch




中学2年生 覚えておくと便利な角度の関係 公式 個別進学教室マナラボ受験 教育情報サイト




二等辺三角形の角度を利用した難問 良問 ラングレー2題 なぜか分かる はかせちゃんの怪しい研究室



角を求める問題




世界一わかりやすい数学問題集中2 4章 平行と合同と証明




二等辺三角形の角度の問題 基礎から応用までパターン別に解説 中学数学 理科の学習まとめサイト




中2数学 補助線 映像授業のtry It トライイット
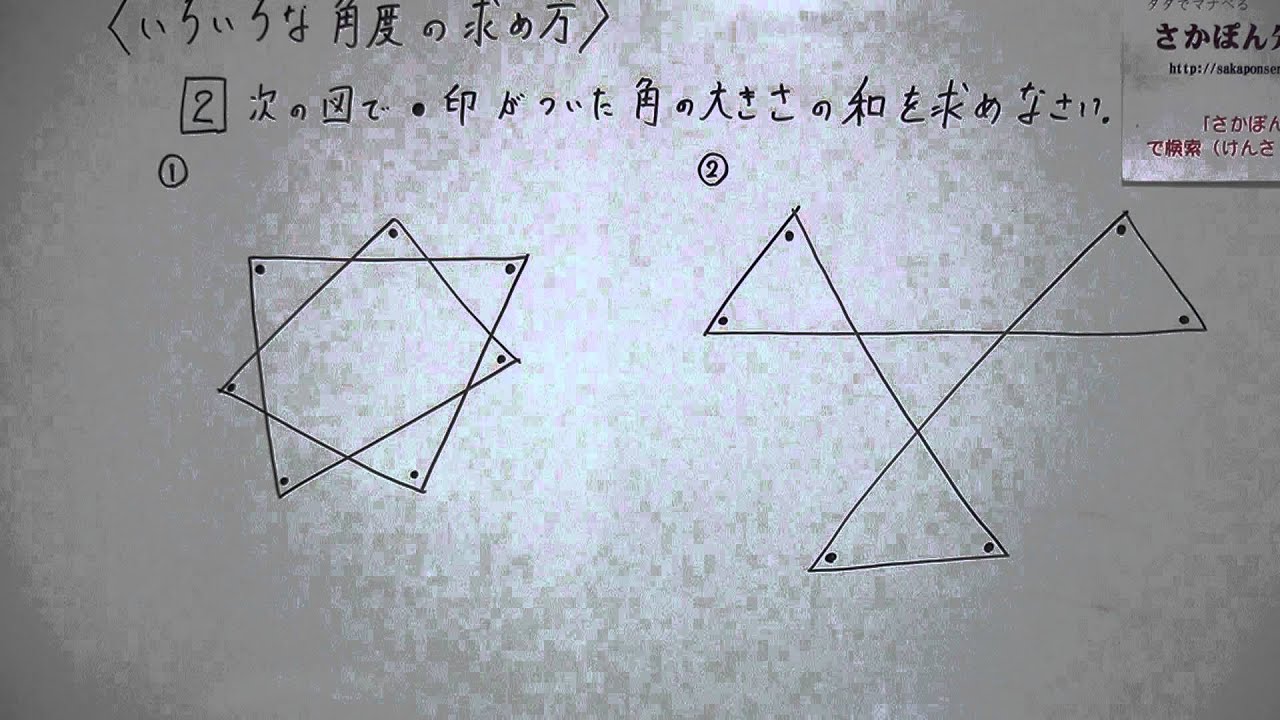



中学校2年生数学 いろいろな角度の求め方




世界一わかりやすい数学問題集中2 4章 平行と合同と証明



補助線の練習



中学二年数学図形の問題です Xの角度の大きさが70 になる理由を教えてくだ Yahoo 知恵袋




三角形の角度 無料で使える中学学習プリント



0 件のコメント:
コメントを投稿